
This choice leads to differences in the time complexity of the algorithm. The algorithm may be modified to start with any particular vertex s by setting C to be a number smaller than the other values of C (for instance, zero), and it may be modified to only find a single spanning tree rather than an entire spanning forest (matching more closely the informal description) by stopping whenever it encounters another vertex flagged as having no associated edge.ĭifferent variations of the algorithm differ from each other in how the set Q is implemented: as a simple linked list or array of vertices, or as a more complicated priority queue data structure. Return F, which specifically includes the corresponding edges in EĪs described above, the starting vertex for the algorithm will be chosen arbitrarily, because the first iteration of the main loop of the algorithm will have a set of vertices in Q that all have equal weights, and the algorithm will automatically start a new tree in F when it completes a spanning tree of each connected component of the input graph.However, for graphs that are sufficiently dense, Prim's algorithm can be made to run in linear time, meeting or improving the time bounds for other algorithms.

In terms of their asymptotic time complexity, these three algorithms are equally fast for sparse graphs, but slower than other more sophisticated algorithms. However, running Prim's algorithm separately for each connected component of the graph, it can also be used to find the minimum spanning forest. These algorithms find the minimum spanning forest in a possibly disconnected graph in contrast, the most basic form of Prim's algorithm only finds minimum spanning trees in connected graphs. Other well-known algorithms for this problem include Kruskal's algorithm and Borůvka's algorithm.

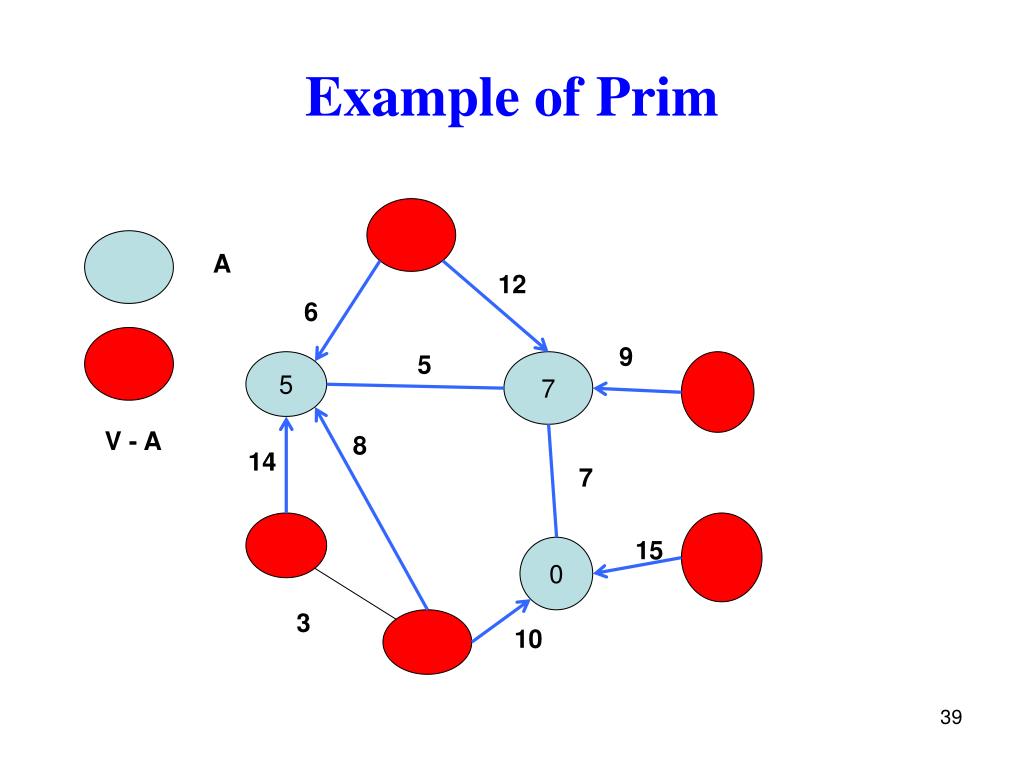
Therefore, it is also sometimes called the Jarník's algorithm, Prim–Jarník algorithm, Prim–Dijkstra algorithm The algorithm was developed in 1930 by Czech mathematician Vojtěch Jarník and later rediscovered and republished by computer scientists Robert C. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. In computer science, Prim's algorithm (also known as Jarník's algorithm) is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. A demo for Prim's algorithm based on Euclidean distance


 0 kommentar(er)
0 kommentar(er)
